[BOJ/JAVA] 백준 15486번 퇴사2 ( DP )

✔ 문제
난이도 : 골드5 🥇
https://www.acmicpc.net/problem/15486
15486번: 퇴사 2
첫째 줄에 N (1 ≤ N ≤ 1,500,000)이 주어진다. 둘째 줄부터 N개의 줄에 Ti와 Pi가 공백으로 구분되어서 주어지며, 1일부터 N일까지 순서대로 주어진다. (1 ≤ Ti ≤ 50, 1 ≤ Pi ≤ 1,000)
www.acmicpc.net

T : 상담하는데 걸리는 기간
P : 상담 했을 때 받을 수 있는 금액
N이 주어젔을 때 오늘부터 N+1일째 되는 날 퇴사를 하기 위해서, 남은 N일 동안 최대한 많은 상담을 하려고 한다.
상담을 적절히 했을 때, 얻을 수 있는 최대 수익을 구하는 문제입니다.
✔ 문제 풀이
단순하게 1일~N일, 2일~N일... 모든 경우를 계산하게 되면 N의 범위가 최대 1,500,000이기 때문에 신간초과가 됩니다.
그래서 DP의 특징인 메모이제이션을 통해 중복연산을 줄이면서 문제를 해결해 나가야 합니다.
하지만 DP문제는 어떻게 적용하는지 떠올리기가 아직까지는 쉽지 않은 것 같습니다.
그렇기 때문에 다양한 문제를 많이 접하면서 풀어봐야 하는 것 같습니다.
그럼 문제를 풀어보겠습니다.
int n = Integer.parseInt(br.readLine());
int[][] schedule = new int[n+2][2];
int[] dp = new int[n+2];
for( int i = 1; i<n+1; i++){
st = new StringTokenizer(br.readLine());
int t = Integer.parseInt(st.nextToken());
int p = Integer.parseInt(st.nextToken());
schedule[i][0] = t;
schedule[i][1] = p;
}💡 n+2
일자를 배열의 인덱스를 통해 표현하기 위해 즉, 인덱스와 일자를 일치시키기 위해 +1,
금액을 완전히 계산되는 날은 n+1일째 이기 때문에 n+1 인덱스에 최종 결괏값을 저장됨으로 +1,
총 n+2 크기의 배열을 선언하였습니다.
int max = 0;
for( int i = 1; i<=n+1; i++){
if( max < dp[i]) max = dp[i];
int next = i + schedule[i][0];
int cost = schedule[i][1];
if( next < n+2 ){
dp[next] = Math.max(dp[next], max + cost);
}
}💡 if( max < dp[ i ] ) max = dp[ i ]
현재 날짜 까지(i) 의 최대 이익을 갱신합니다.
💡 dp[ next ] = Math.max( dp[ next ], max + cost )
dp[next] : 이전에 다른 상담 일정을 통해 설정된 next날까지 왔을 때의 이익
( 다른 상담을 선택했을 때의 이익 )
max + cost : 현재 날짜까지의 최대 이익(max)과 현재 상담 비용(cost)을 더한 값
( 현재 상담을 선택했을 때의 이익 )
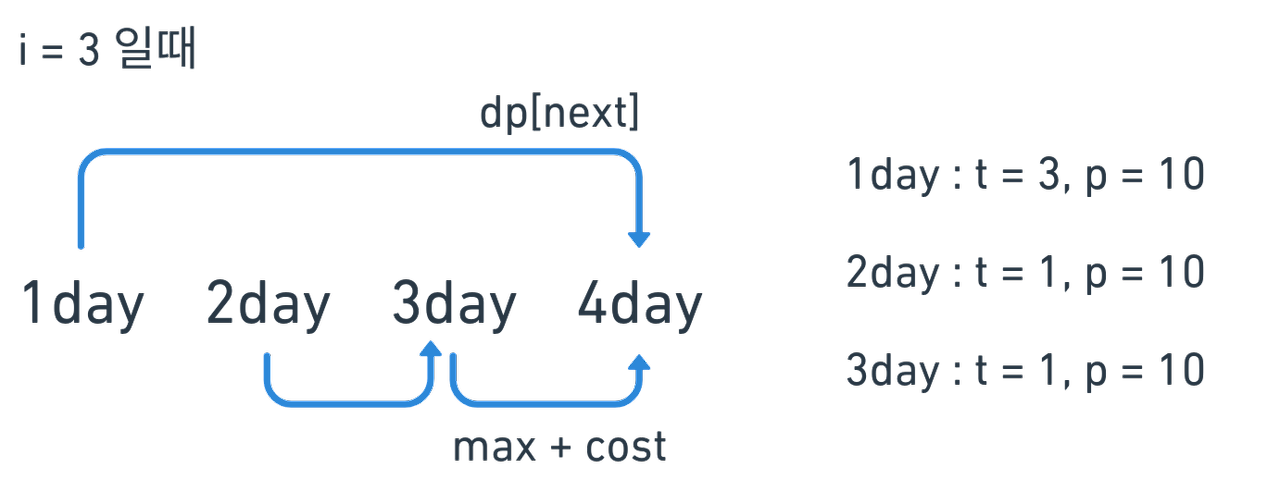
두 가지 값 모두 next날까지의 상담 이익을 의미합니다.
하지만 어떤 상담 일정을 통해 next날까지 왔는지에 따라 상담 이익이 달라지게 되고, 그 이익중 가장 큰 이익을 얻을 수 있는 상담 일정을 선택하는 과정입니다.
이렇게 함으로써 현재까지의 최대 이익을 유지하면서, 다음 상담을 고려하여 최대 이익을 갱신할 수 있습니다.
🔎 전체 코드
import java.io.IOException;
import java.io.BufferedReader;
import java.io.InputStreamReader;
import java.util.StringTokenizer;
public class Main{
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader( new InputStreamReader(System.in));
StringTokenizer st;
int n = Integer.parseInt(br.readLine());
int[][] schedule = new int[n+2][2];
int[] dp = new int[n+2];
for( int i = 1; i<n+1; i++){
st = new StringTokenizer(br.readLine());
int t = Integer.parseInt(st.nextToken());
int p = Integer.parseInt(st.nextToken());
schedule[i][0] = t;
schedule[i][1] = p;
}
int max = -1;
for( int i = 1; i<=n+1; i++){
if( max < dp[i] ) max = dp[i];
int next = i + schedule[i][0];
int cost = schedule[i][1];
if( next < n+2 ){
dp[next] = Math.max(dp[next], max + cost);
}
}
System.out.print(dp[n+1]);
}
}